arrow_back In the following picture;

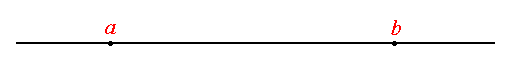
The distance between a and b is b-a.

Now in the next picture;

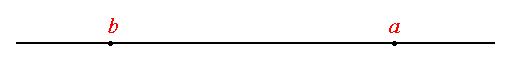
This time, the distance between a and b is a-b.

Now, in general, if we are given a and b but we don't know which of them is bigger, then the distance is going to be one of b-a or a-b.

It will be whichever one is positive. In other words, the distance between a and b is whichever one of a-b or -(a-b) is positive. And this is exactly what

|a-b|

is! That's why we use absolute values so much in analysis, because they are the right way to measure distance between real numbers.

Later on, we'll see the way to measure distance between complex numbers, vectors and even functions. In all of these cases, the distance measurements will be closely analogous to the absolute value function.

By the way, while the distance between a and b is |a-b|, it's equally true that the distance is |b-a|, since these two expressions are the same.

Click here to return to the main page.