arrow_back In this case, the function attains its maximum value at one of the endpoints of the interval on which it is defined. Lemma 6.13 needs the function to be differentiable as a function on D at the point at which it attains its maximum. This means that f has to attain its maximum at an interior point of D. (Remember that part of the definition of differentiability is that the point in question has to be an interior point of the domain.)

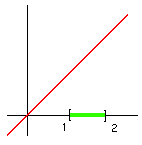
Thus, although f is differentiable, as a function on the whole real line, at the point x=2 it is not differentiable as a function on [1,2]. Yet we can only call x=2 a maximum of f as a function on [1,2], which explains why it is inappropriate to apply Lemma 6.13 to this situation.

In fact, the purpose, from a technical point of view, of the requirement that f(a)=f(b) in Rolle's Theorem is precisely in order to ensure that at least one out of the maximum or minimum of the function lies in the interior of the interval, so that we can apply Lemma 6.13.