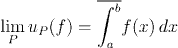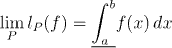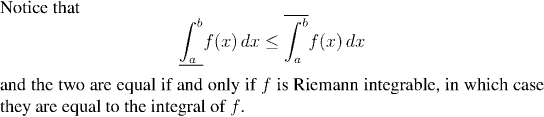 Before giving the proof, we shall introduce a useful notation. Recall the the upper and lower Riemann sums of a bounded function always converge to some limits. (If the function is not Riemann integrable, the two limits are not equal, but they still exist.) We shall call the limits of the upper and lower Riemann sums respectively the upper and lower Riemann integrals and write them:
Before giving the proof, we shall introduce a useful notation. Recall the the upper and lower Riemann sums of a bounded function always converge to some limits. (If the function is not Riemann integrable, the two limits are not equal, but they still exist.) We shall call the limits of the upper and lower Riemann sums respectively the upper and lower Riemann integrals and write them: