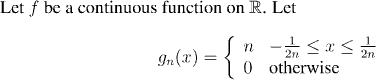arrow_back We'll discuss here how to choose a sequence of functions converging to a given function f. This discussion should make the construction of the approximating sequence in the proof easier. But, it will not give any indication of why the sequence of functions is actually a polynomial. That is a very clever insight which you'll see in the main proof.

Question: What does the graph of g_n(x) look like as n increases?

Here is the graph of f(n).

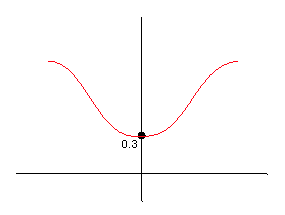
Question: Sketch the graphs of f(x) g_n(x) and compare it with the graphs of g_n(x) and f(x). Judging by the graph, what do you think 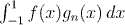converges to?

Question: Now, what we really want is to have a sequence of functions converging to f. Can we use this last observation to make some functions that converge to f(t)?