arrow_back arrow_forward

Class Contents

• The least upper bound of a set
• The least upper bound property
• The axioms of the real numbers

The Least Upper Bound of a Set

• A set need not have a supremum just because it is bounded above, but in order for it to have a supremum, it must, in particular, be bounded above.
• If a set has a greatest element then that greatest element is the supremum of the set. On the other hand a set may have no greatest element and still have a supremum (for example, this set studied in Class 4).

The next two examples show sets which are bounded above, but which do not have supremums. The second is more profound, but in both cases one feels that the reason they don't have supremums is because something is missing from the set X. In other words, if X has sets with no supremum, then something is "wrong with" X!

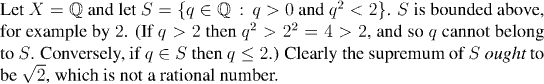
We'll prove that this last set has no supremum in the rationals later on, after we have the definition of the real numbers to work with. Bearing in mind the idea that if X has sets with no supremum then it must be because it is missing things, we make the next definition.

Least Upper Bound Property

Note:

The requirement that the sets be non-empty is important. Notice that every element of X is an upper bound for the empty set. So, provided X has no smallest element (which is typically the case), the empty set cannot be relied on to have a supremum.

In practice, when one uses the least upper bound property, one always has to remember to check that the set being considered is nonempty. Failing to do this is a common mistake. In some theorems, one wants to use the least upper bound property to show that a set has a supremum, and it turns out to be quite hard to check that the set is non-empty.

The Axioms of the Real Numbers

The real numbers are an ordered field with the least upper bound property.

The rational numbers do not have the least upper bound property

The natural numbers have the least upper bound property.

In the next section we shall look at how these two axioms of the real numbers are used, and begin to build up the important properties of the real numbers.