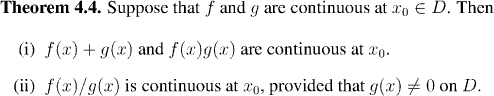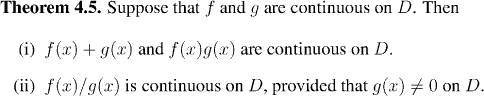Class Contents

Interactive demonstration

1. It's important that a belongs to D. Otherwise f(a) might not exist.
2. It would make sense to say that f is continuous at a provided f(x) goes to f(a) as x goes to a. There is a tricky obstacle to this, which has to be examined in a little detail:
   • Continuity is defined for a being a member of D
   • The limit of f(x) is defined for x being a limit point of D.
   Now a might belong to D, yet not be a limit point of D. In this case, a is called an isolated point. For the record:

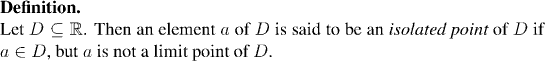
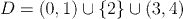
The point 2 is an isolated point of D.

1. If a is an isolated point of D then there is a positive d such that a is the only element of D in (a-d, a+d)
2. It follows that if a is an isolated point of D then every function is continuous at a, because, if we choose d small enough then the only point of D that satisfies the condition |x-a|< d is a itself (and the condition |f(x)-f(a)|< e is always satisfied when x=a)
3. On the other hand, if a is a limit point, then f(x) is continuous at a if and only if f(x) converges to f(a) as x goes to a.

We can summarize all this in the following rule:

The following criterion is one of the most useful ways of showing a function is continuous at a point. Note that it holds irrespective of whether a is a limit point or not.

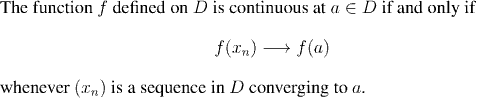
So, in order to show a function is continuous, a standard approach is to suppose that we are given an arbitrary sequence (x_n) converging to a, and to show that f(x_n) converges to f(a). The importance of this is that we have reduced continuity of functions to convergence of sequences which is often easier to handle. Look out for this approach in the examples and proofs that follow.

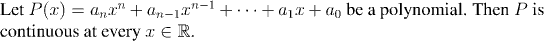
Every point of R is a limit point, so to prove continuity we must prove that P(y) converges to P(x) as y goes to x. But this follows immediately from Theorem 4.1.

This last example serves to point out two useful facts:

1. Theorem 4.1 is perfectly poised to prove results about the arithmetic of continuous functions.
2. Many functions are continuous not just at one or two points, but at every point in their domain. Such functions are simply called continuous.

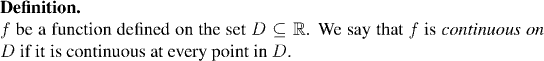
Our results about the arithmetic of continuous functions are:

Both of these are straightforward applications of Theorem 4.1.. In the case that the point under consideration is an isolated point then, as we saw, all the functions in question are automatically continuous, so there is nothing to prove.

Special functions

Functions like sin(x) and cos(x) are still a long way ahead of us, but we are now in a position to make a little digression, and introduce the exponential functions. From this, we can then introduce the logarithmic functions in Homework 6.

After this digression, we return to studying limits of functions, by focussing on an important special type of limits: the derivatives, and we study the differentiable functions.