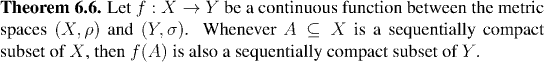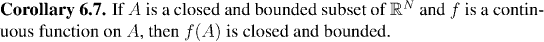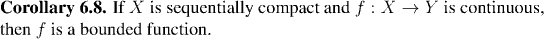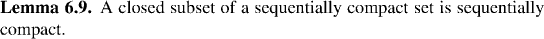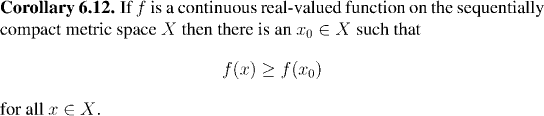arrow_back arrow_forward

Class Contents

• Properties of sequentially compact sets
  • Continuous functions are bounded on sequentially compact sets
  • Invertible continuous functions on sequentially compact sets
  • Continuous functions attain their bounds on sequentially compact sets
  • Continued in the next class...

Properties of Sequentially Compact Sets

Continuous functions are bounded on sequentially compact sets

Sequentially compact sets are important because continuous functions defined on sequentially compact sets have some very useful properties, which they do not have in general when defined on non-compact sets. These include being bounded, and having points at which they reach their maximum and minimum values. In this section we shall prove most of these properties, which, in the main, follow quite quickly from the definition of sequential compactness. We can rely on the results of the last section to tell us that sequentially compact sets are very common, and to help us recognize them in practice.

Proof.

Now, if A is closed and bounded in Euclidean space then by Theorem 6.5, it is sequentially compact. Theorem 6.6 says that any continuous image of A must be sequentially compact, and so by Proposition 6.4, the image is also closed and bounded. In general the continuous image of closed sets isn't closed, but this example shows that quite often continuous functions on Euclidean space (in particular, on the real line) will map closed set to closed sets. We summarize this fact in a corollary:

In general, if a continuous function is defined on a sequentially compact set then its range will be sequentially compact. Thus, since the range will be a bounded set (again by Proposition 6.4), the function will be bounded:

We shall study C[a,b] in depth in subsequent chapters, and shall even work an extended example with it later in this chapter.

Invertible continuous functions on sequentially compact sets

Suppose that f is a continuous function from X to Y, which is one-to-one and onto (also called bijective). Then f has an inverse function from Y to X. It seems very reasonable to expect that since f is continuous then its inverse will also be continuous. After all, we are thinking that y=f(x) is going to vary continuously as x varies, so surely, x will vary continuously as x varies.

It is a very surprising fact, that the definition of continuity alone, does not ensure that the inverse of f will necessarily be continuous! Fortunately, in most of the situations that interest us, we can show that the inverse of a continuous function will still be continuous. But to do that, we need an extra ingredient, which is usually provided by compactness.

Because it seems implausible that there is a continuous invertible map which does not have a continuous inverse, we'll start with an example to show that this really can happen. However, although an example is convincing, it doesn't necessarily show why this unexpected turn of events is coming about.

So after the example, we'll see what happens if one sets out to prove that the inverse of a continuous function must be continuous, using only the definition of continuity. The logical problems that we run into when we try this illustrate why, after all, it is not so surprising that the inverse of a continuous function need not be continuous.

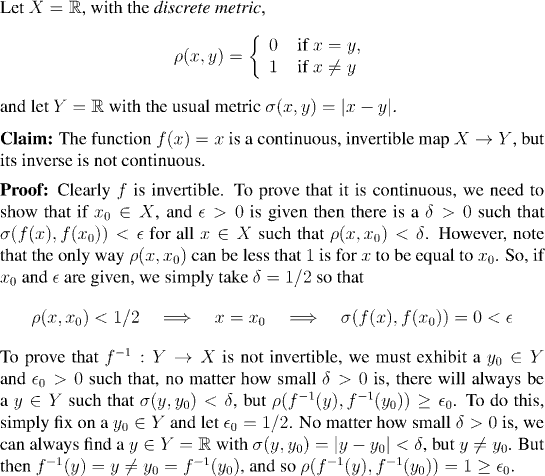
The extra hypothesis that we need in order to show that the inverse is also continuous, is that f be defined on a sequentially compact set. Proposition 6.10 will prove that, but first we need a lemma, which is also useful in its own right for recognizing sequentially compact sets.

Proof.

Proof.

As an application of this result, we can give a quick proof of the fact that the logarithmic functions are all continuous.

Continuous functions attain their bounds on sequentially compact sets

In Corollary 6.8 we saw that a continuous function defined on a sequentially compact set is always bounded. In fact, something much stronger is true: A continuous function defined on a sequentially compact set has a point at which it attains its greatest value. Thus, not only does sup(f(X)) exist, but there is an x₀ at which f(x₀)=sup(f(X)).

Put another way, this says that when a continuous function is defined on a sequentially compact set, it has a maximum. Not surprisingly this fact has important implications for studying differentiable functions, where maxima and minima of functions play an important role. In the present section we shall prove this result, and in the next, we shall apply it to prove the Mean Value Theorem, which is the most important tool for understanding real differentiable functions.

Proof.

Of course, by applying the proposition just proved to -f in place of f we immediately obtain the corresponding result for minima:

Continued in the next class...