arrow_back arrow_forward

Class Contents

• Compactness and sequential compactness are equivalent (continued)

Compactness and Sequential Compactness are Equivalent (continued)

On with the proof of Theorem 6.24

Our standing assumption throughout the remainder of this section will be that X is a metric space and that K is a sequentially compact subset of X. Our aim will be to show that K is compact. To this end, suppose further that we have been presented with a fixed open cover U of K. Our job will be to show that we can pick out a finite cover of K consisting of points of U.

Proof.

Claim: We can use Lemma 6.25 to find a sequence (x_n) of points in K which can get arbitrarily close to any point in K. To do this, we use the following construction:

We call the set of points (x_n) a countable, dense set.

Now we use the x_n to select out a collection of open sets from the open cover which we can work with.

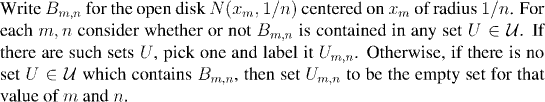
Claim: The sets U_{m,n} cover K.

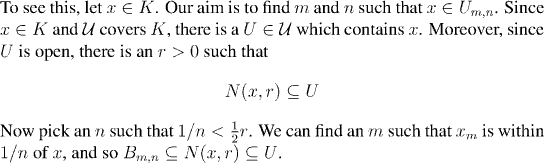
The picture shows the details of this clearly:

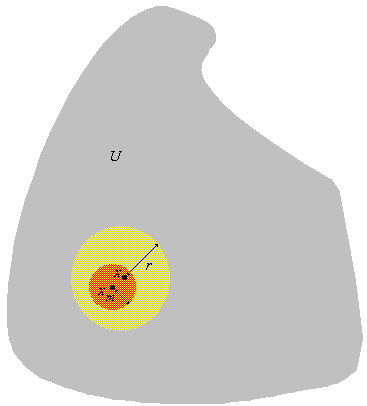
Question: Work out the details of why B_{m,n} is contained in U.

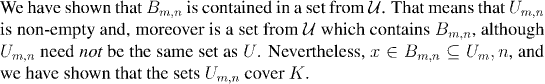
We are now ready for the main part of the argument. We shall show that finitely many of the U_{m,n} will cover K. Since the non-empty U_{m,n} all come from U, this will prove our result.

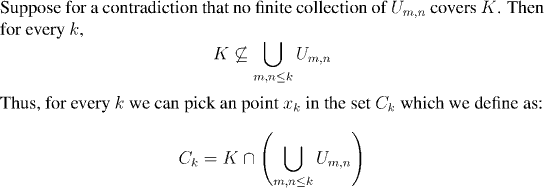
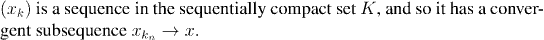
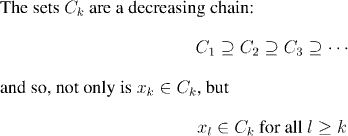
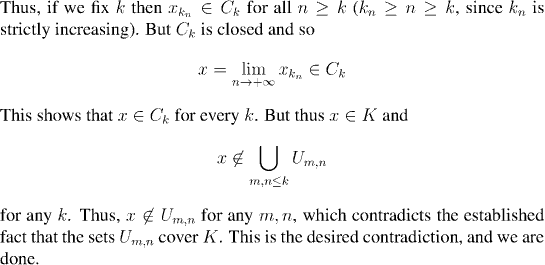
The next class, which is the last one of this chapter, will introduce a new property of metric spaces: completeness. This allows us to answer the question "When does a sequence converge?", without knowing in advance what it is supposed to converge to.