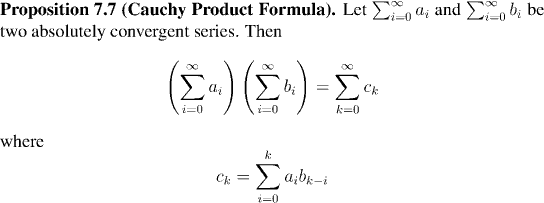
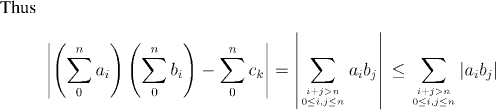We can think of the set of all i,j between 0 and n
as the shaded region on the grid:
Then the set of pairs that we sum over to get the sum of the ck's is:
The remaining terms are the summation over the region:
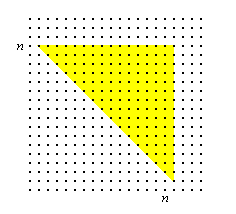
We are trying to show that as n grows, the summation over this region goes to zero. The trick is to notice that although the region grows in size as n grows, the terms that belong to the region lie further and further out. We shall show that the upper triangular region lies inside the larger "L-shaped" region shown below, and make an estimate of the summation over that region.
(Notice for the estimate below that this last shape is obtained by taking a square of side n and deleting a square of side n/2 from the corner.)
