Class Contents
- Properties of E(z)
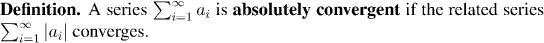
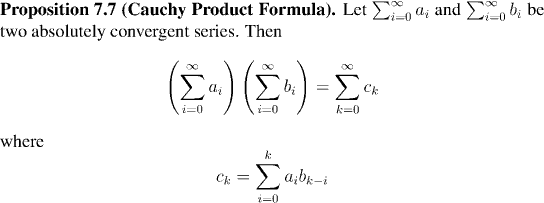

Remembering that our aim is to show that E(x)=ex, we can see how to go a large step of the way using Corollary 7.8:
Remark:
In other words, we need to know that E(x) is continuous. In fact we shall do more than this. We shall show that E(x) is differentiable, and, of course, differentiable functions are continuous.
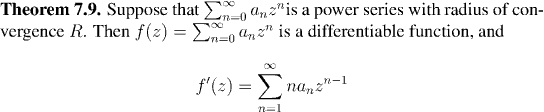
 What does it mean to differentiate a complex function?
What does it mean to differentiate a complex function?
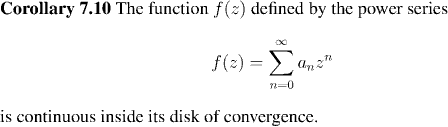
 For the proof of this result, just check that the proof of
Proposition 4.8
works perfectly well for complex differentiation.
For the proof of this result, just check that the proof of
Proposition 4.8
works perfectly well for complex differentiation.
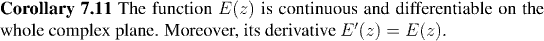 In view of the ideas we discussed above, Corollary 7.11 allows us to conclude:
In view of the ideas we discussed above, Corollary 7.11 allows us to conclude:
 Now we have a power series, which is perfectly well defined for all complex numbers, and we know that it agree with ex for all values x for which ex has so far been defined. We use this to now extend our definition of exponentiation to the whole complex plane:
Now we have a power series, which is perfectly well defined for all complex numbers, and we know that it agree with ex for all values x for which ex has so far been defined. We use this to now extend our definition of exponentiation to the whole complex plane:
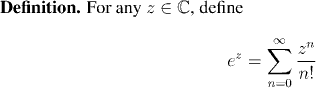
The payoff from this extension of our definition, together with all that we know about power series (specifically Theorem 7.9) will be:
- The ability to obtain new insights into existing functions: we shall show that general power functions, logarithmic function, and exponential functions are all differentiable.
- Constructions for a whole new class of important functions: the trigonometric functions.


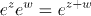 :
:
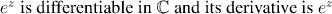 :
: