Class Contents
Power Series
Now we turn to the best behaved types of series, and the most important for applications: power series.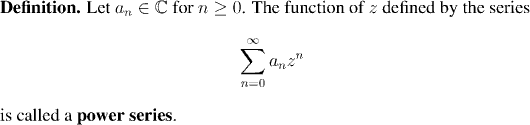 Power series are very commonly used to define functions. In fact, in
this course the standard functions of analysis, sin(x), cos(x)
and e^x will all be defined in terms of power series. Since a
power series can only define a function at points for which the series
converges, it is important to be able to tell where our power series
converges, and where it diverges. The following theorem gives a
wonderfully simple answer to this question.
Power series are very commonly used to define functions. In fact, in
this course the standard functions of analysis, sin(x), cos(x)
and e^x will all be defined in terms of power series. Since a
power series can only define a function at points for which the series
converges, it is important to be able to tell where our power series
converges, and where it diverges. The following theorem gives a
wonderfully simple answer to this question.

Remark:
-
The set of z which satisfy this condition for convergence is an
open disk in the complex plane;
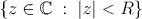
This disk is called the disk of convergence of the series, and R is called the radius of convergence.
- Notice that Theorem 7.6 is silent on the question whether the power series converges for values of z with |z|=R. The answer is that it is possible for the power series to diverge at some such values, and converge at others. The exact behavior is delicate, and depends heavily on the particular function under question. There are theorems in complex analysis and function theory which look into the behavior on the boundary of the disk of convergence in more detail.
The Exponential Function
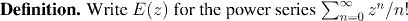
Factoid:
The power series for E(z) converges for all complex z.
(i.e. its radius of convergence is infinity).
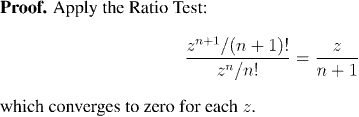 We are now aiming to show that the power
series E(x) is equal to the exponential function
ex for all real numbers x. (Remember that we have already
defined the number e to be E(1).)
We are now aiming to show that the power
series E(x) is equal to the exponential function
ex for all real numbers x. (Remember that we have already
defined the number e to be E(1).)This result is really extremely deep (perhaps the deepest result so far in this class!) The fact that ex can be expressed as a power series enables us to show that exponential functions (and logarithms) are differentiable and to calculate their derivatives.
Moreover, note that although ex has, so far, only been defined for real x, the power series E(z) is defined for all complex numbers. Once we know that E(x)=ex for all real x, it makes sense to define ez as E(z) for all complex numbers. This then becomes the basis of our definition of the functions sin(x) and cos(x) , by means of the formulae:
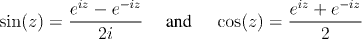
The first big step to showing that E(x)=ex, will be to show that the power series E(z) has the same multiplicative properties that we associate with exponential functions, namely that E(z)E(w)=E(z+w).
Remark:
Before going into the details of the proof,
click to see the
idea
of the argument for why the function E(z) should have this property. Once you've studied that, we'll see why the next theorem is the right formulation of a useful property of series.