Class Contents

Tests for Convergence

The two tests which we present here are the Ratio Test and the Root Test. Both of them present criteria which boil down to meaning that the series satisfies the Comparison Test agains a certain geometric series. Although the test yields a comparison with a fairly simple convergent series, the criteria, especially of the ratio test, are sufficiently easy to apply, that these tests are useful first checks to see whether or not many common series converge.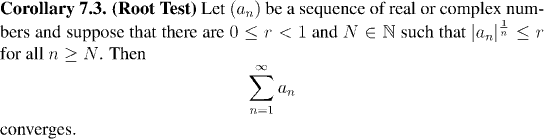

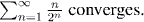
Proof.

Example:

Question: Check this using the Ratio Test.

Example:

Question: Check this using the Ratio Test.

Example:

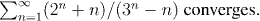
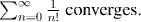
Question: Check this using the Ratio Test.

You may recognize the series in the last example from calculus. This series converges to the number e, which will be the basis of our development of not only the exponential functions and logarithms, but also of trigonometric functions.

It's important to bear in mind that we have not yet had any definition of e in our development of analysis. Now is the point where we see this number for the first time, and we shall pause for a second to record a formal definition:

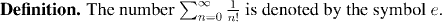The number e is very important -- we shall prove that for real x, the series

where e^x is the regular operation of exponentiation developed in the earlier chapters. This will give us a totally new way of viewing exponentiation, and difficult results which we could not prove otherwise will become quite easy.

All of this is accomplished with the help of power series, which we shall study in a short while.

Series of Reciprocals

An important source of examples of convergent series are the series of the form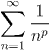

for p a variable real number. We shall show that these series converge when p is greater than 1 and diverge when p is less than or equal to 1. Thus in a not-too-precise way, the sum of 1/n marks the "edge of the envelope" for convergent series: in order for the series to converge, its terms must decay at least as fast as 1/n.

Remark:

Series of non-negative terms are particularly nice to work with. Note that the partial sums of such a series form an increasing sequence. Thus, the partial sums (and so the series itself), converge if and only if they are bounded above.

To show that a series of non-negative terms converges, it is enough to show that the partial sums are bounded. This will be useful in proving Theorem 7.5.

Proof of Theorem 7.5.