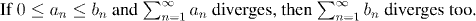Class Contents
Aims:
The aim of this chapter is to develop some of the special functions of analysis, such as the exponential function ex, and the trigonometric functions, especially sin(x) and cos(x). We shall define these functions and discover some of their most basic properties (such as the fact that sin(x) is periodic, and that it has a zero -- this will be our definition of the number pi).We will construct all of these functions using infinite series, so the first part of the chapter is devoted to the basics of series. Series are a powerful mathematical concept, which are useful for constructing functions, and have a fascination in their own right. We shall start by aiming quickly towards the important uses of series, but as we become more familiar with them, we shall also explore some of the remarkable features of the more unusual series.
Series
Let (an) be a sequence of real or complex numbers. What does it
mean to talk about the sum of all of these terms:
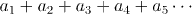
We can't just say that it is the number we get when we add all of the terms together. For one thing, that would involve infinitely many operations, and the process would never be done. Instead we use the idea of a limit to say that s is the value of the sum if, as we add more and more of the numbers together, we get closer and closer to s.

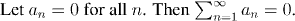
Note that the fact that we are assigning a value to the series includes the implicit assumption that the series converges, and that this number (zero in this case) is the limit.
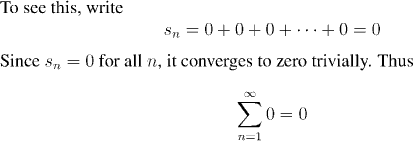
Notice that we avoided any discussion of the sort: "We're adding zero to itself infinitely many times, so this is the same as infinity times zero, and infinity times zero is...?"
The fact that sidesteps this inconclusive line of speculation is one of the strengths of the definition of infinite series.
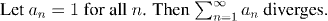
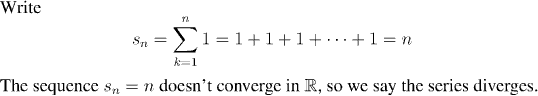
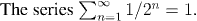
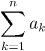
are called the partial sums of the series. A series converges if its sequence of partial sums converges.
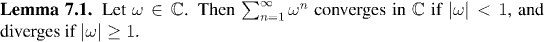 Although it is virtually impossible to calculate explicit formulas for the partial sums of series, nevertheless it is quite easy to determine the convergence or divergence of a huge variety of series. There are a number of "convergence tests" which can be applied to the terms of a series and give effective computational tools for dertermining convergence. Underpinning almost all of these is the following result, the
Comparison Test for Series. This may well be the single most important result in the convergence of series. (And look out for the roles that the Cauchy sequences, and the completeness of the real numbers, play in this theorem.)
Although it is virtually impossible to calculate explicit formulas for the partial sums of series, nevertheless it is quite easy to determine the convergence or divergence of a huge variety of series. There are a number of "convergence tests" which can be applied to the terms of a series and give effective computational tools for dertermining convergence. Underpinning almost all of these is the following result, the
Comparison Test for Series. This may well be the single most important result in the convergence of series. (And look out for the roles that the Cauchy sequences, and the completeness of the real numbers, play in this theorem.)
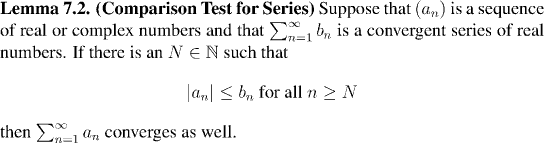
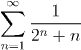
converges.
This follows by the comparison between the terms of this series and the series 1/2n.
Note that although it is easy to see that this series converges, by the Comparison Test, it is impossible to find a simple formula for the partial sums of the series. For that matter, it is not at all easy to say what the series converges to.