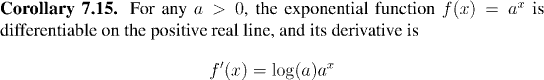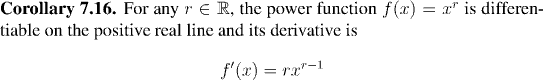Class Contents
Exponential Functions
We are now in a position to use the amazing relationship between exponentiation and power series to prove a number of important results very quickly. In the next class we shall use the exponential functions to define and analyze the trigonometric functions.The first thing we shall do is show that the logarithm base e is differentiable. This is a straightforward application of the Inverse Function Theorem.
Remark:
Since the key to understanding all exponential maps is the special map ex, exponentials and logarithms with this base play a key part in pure mathematics. They are so central to analysis, that we write
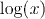
for the logarithm base e (i.e. we don't need a subscript e). This is also the reason that logarithms base e are called natural logarithms.
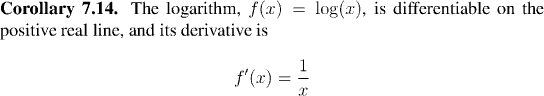We already know that the function ex is differentiable on the real line, and that it is equal to its derivative. We shall extend the result to differentiating general exponential functions:
