arrow_back arrow_forward

Class Contents

• Properties of the Trigonometric Functions

Properties of the Trigonometric Functions

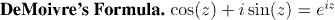
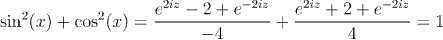
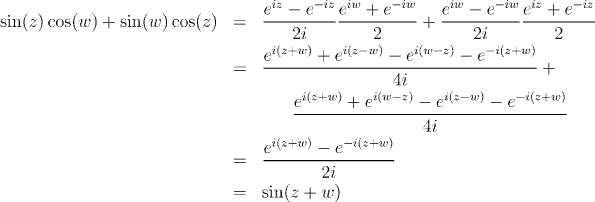
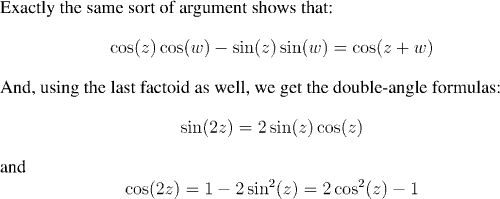
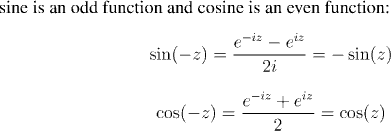We define sine and cosine as complex-valued functions of a complex variable. All of the above properties hold for any complex numbers z and w.

However, an important property of sine and cosine (although one that is so obvious in the gemoetric treatment that it is hardly worth noting) is that when their argument is real, then they take real values. We shall verify that this is the case, and, in the process establish power series expressions for sine and cosine.

Proof.

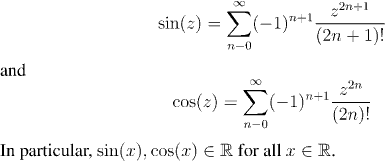
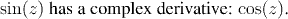
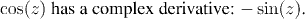
The Chain Rule holds for complex derivatives, and so, since we know the derivative of e^z, the derivative of sin(z) is

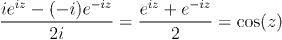
The argument for the derivative of cos(z) is analogous.

The most striking aspect of the trigonometric functions which is still missing from the picture is that they are periodic. We need to show that there is a number a such that sin(x+a)=sin(x) for all a. (In fact, the number a is 2Pi, but we don't even know what Pi is yet!)

To show that sin(x) is periodic, by using the addition formulae for sine and cosine, we need to have

sin(z+a)=sin(z)cos(a)+sin(a)cos(z)

and so, we seek a number a such that

• sin(a)=0, and
• cos(a)=1

Of course a=0 satisfies this, but at the moment it is not even apparent that there are any positive numbers for which sin(z)=0. Thus, our first aim is to study the zeros of sin(z).

Proof.

Proof.

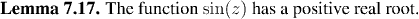
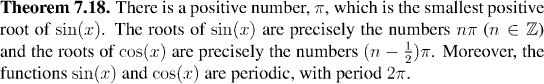
Polar Form for Complex Numbers

One geometric definition of sin(x) and cos(x) is the coordinates of points on the unit circle. We can recover this viewpoint, with the following result: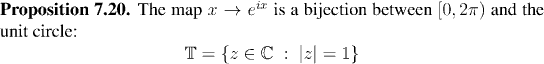

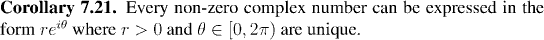Proof.

Proof.

We can use this "polar form for complex numbers" to define the logarithm of a complex number.

Think for a minute about what you would expect the logarithm of a complex number should be. Bear in mind that the fundamental property for logarithms is that

log(x+y)=log(x)+log(y)

and that every complex number can be expressed as

re^(it)

Question: What do you think the logarithm of re^(it) should be?