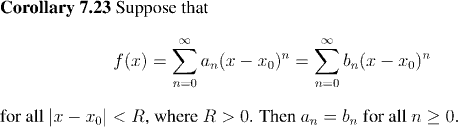
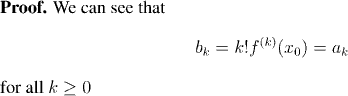
Remark:
We didn't need to assume that the two series had the same radius of convergence, as long as
both of them had positive radius of convergence. By applying the
argument above for the smaller of the two radii of convergence, you deduce that
the coefficients of the two series are the same (and so the radii of convergence had
to be the same). On the other hand, we do need to assume that the two power series
are centered on the same point x0.