 Transcendental numbers are not easy to find. Liouville showed that the number
Transcendental numbers are not easy to find. Liouville showed that the number
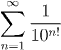
(and others like it) is transcendental. But this number isn't really one that crops up ina natural way. It has been shown that $e$ and $\pi$ are both transcendental, but the proofs are quite hard. Other numbers have been shown to be transcendental by very sophisticated means. For example the proof that
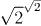
is transcendental was only discovered in the past thirty years.
Nevertheless it is quite easy, using the concept of countable and uncountable sets, to prove that there are infinitely many transcendental numbers. Even, that there are more transcendental numbers that algebraic numbers (the algebraic numbers are the ones which are not transcendental).