arrow_back arrow_forward

Class Contents

• Estimating e and Pi
  • Estimating from above
  • Estimating from below

Estimating e and Pi

The numbers e and Pi have shown themselves to be of fundamental importance in understanding basic functions of analysis (such as sin(x) and cos(x)). Yet we so far have no concrete idea of what their values are. Both e and Pi are irrational numbers (in fact they are transcendental ). We shall show that e is irrational in this section; it is much harder to prove that Pi is irrational, but we shall do that later. We shall also estimate the values of e and Pi, so that we have some reasonable approximations to help our understanding of them.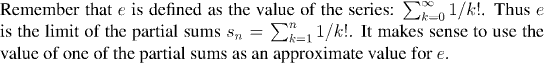 How accurate would an approximation by one of the partial sums be? 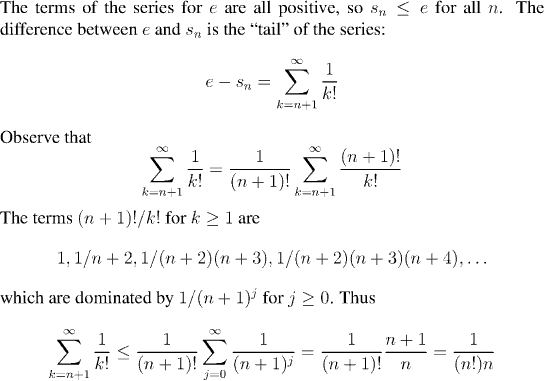This shows that the greatest error we have in approximating e by the n^th partial sum is

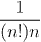
Now 10 x 10! is over 30 million, so the estimate that we get with just the tenth partial sum is already accurate to within 1 part in 30 million. When we calculate the partial sum we find:

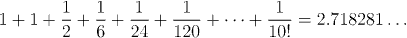
Since the total error is less than 0.000001, we can be confident that all the digits (except possibly the last one) are accurate. Thus gives us an estremely accurate estimate of e. This is much better than we shall do for Pi!

What is also quite remarkable, is that the same estimates which showed how accurate our approximation to e was, will also serve to show that e is irrational.

Proof.

Now we turn to the problem of estimating Pi. We shall use the fact that Pi/2 is the first positive zero of cos(x).

References: Taylor's theorem | Power series for cos(x)

Estimating from above

References: Intermediate Value Theorem

Estimating from below

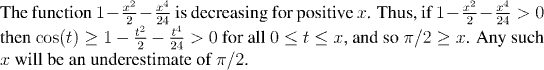
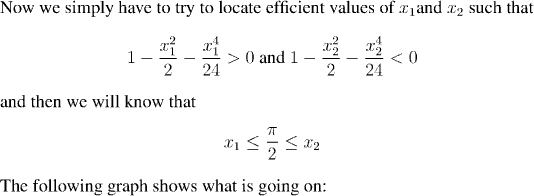
To make the result, rigorous, one can verify by by looking at the graph (which was drawn by Maple), or by direct calculation (using a pocket calculator, or even by hand) that x_1=1.3 and x_2=1.7 satisfy the appropriate inequalities. We summarize these reults in a proposition: Sharpening the upper bound in this argument would be very easy: just add in more terms of the Taylor series. After all, we only need to locate a point where the polynomial is negative, and by the Intermediate Value Theorem, that is our estimate. Pushing the point down when we have a higher degree polynomial would be no trouble, and we could obtain estimates that were close to 3.1415...

The problem is with the lower bound. The argument for the lower bound involved the fact that our polynomial was decreasing. This won't be so easy to see when we add in more terms. In fact, it will only be locally decreasing, and even that would be very hard to prove. We will see other ways of sharpening our estimate for Pi later -- for the moment this rough estimate must serve.