Class Contents
Continuous Functions and Connected Sets
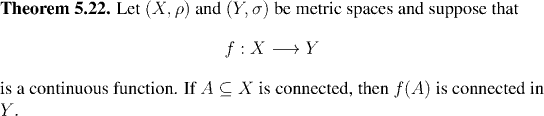
We can combine our particularly good understanding of connected subsets in the real line with Theorem 5.22. On the face of it, all this says is that the continuous image of an interval is also an interval---cute, but perhaps not very useful.
However, if we combine this with the defining property of an interval, we obtain an extremely useful theorem indeed: the Intermediate Value Theorem.
We start by proving the theorem, and the remainder of the chapter will be taken up with two applications of this theorem: a quick construction of the logarithmic functions, and a method for calculating roots of equations.
Of course, if f(a) is greater than f(b) then an analogous result with f(a) > y0 > f(b) holds.
Applications
The logarithm
In Homework 6 we constructed the logarithm base a and derived some of its properties.If we look at what was being asked in the homework assignment, we can see that what the first two questions establish is that the exponential function f(x)=ax is invertible.
The method used was to pull a formula for the inverse, g(x), out of thin air (and a pretty unfriendly formula to work with it was too) and then verify that it had the right properties. In fact, Question 2(a) does no more or less than to ask you to show that g(f(x))=x, and Question 2(b) asks you to prove that f(g(x))=x. Taken together these two facts are exactly what is needed to conclude that f(x) is invertible and that g(x) is its inverse.
The last part of Question 2 establishes the familar properties of the logarithm. But if you look at Homework 6 you'll see that the proof uses no properties of the logarithm other than the fact that the logarithm is the inverse of the exponential function, coupled with some properties of the exponential function.
In this section we shall show that the exponential function is invertible, in a much quicker way. Our proof will demonstrate the use of the Intermediate Value Theorem for showing that functions map onto the reals or some other useful set.


The method of bisection
The method of bisection is a very simple and effective means of
estimating the roots of equations. Unlike other methods for finding
roots, which may be faster, this is the only method which is
guaranteed to work for all continuous functions.
The theoretical underpinning of the method of bisection is the Intermediate Value Theorem. This tells us that if we know that a function is positive at one point, and negative at another, then a root of the function (a point at which it is zero) must lie between these two points.
As an example of how to use this algorithm, we shall approximate the square root of 2 to within 0.1.

