Class Contents
Connected and Disconnected Sets

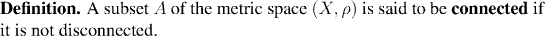
The point of this definition is that when a set falls into two disconnected pieces in a natural way, then we can separate the two pieces from each other by disjoint open sets. For example, consider the set A shown below. This is a subset of the plain, consisting of two pieces. Click on the picture to see how to the two pieces can be separated by open sets:
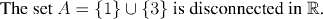
The following picture shows the set A:

Question: Draw a picture of sets which would disconnect A.
Although in practice it may be hard to find open sets which disconnect a given set, at least there is a fairly straightforward task which has to be accomplished in order to prove disconnectedness in any given case.
Not so for proving connectedness, for which one would have to show that there is no choice of two open sets U and V which satisfy the criteria to disconnect the set. Thus, the usual strategy for proving a set is connected is to suppose the opposite and search for a contradiction. The next theorem is particularly useful, because it tells us precisely what the connected sets of real numbers are.
But first we need a definition.
The intervals are just the sets we know of the form (a,b) or [a.b] or (a,b] etc. We want a single unifying property that we can use to characterize all the intervals of the different kinds (open, closed, half open, etc). The following property does the job, and in fact we make it our definition of the term "interval".
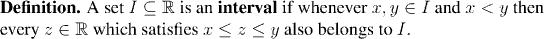
And now for our theorem:
Proof of Theorem 5.21:
 If I is not an interval then it's not connected
If I is not an interval then it's not connected
 If I is an interval then it is connected.
If I is an interval then it is connected.
The real line is quite unusual among metric spaces in having a simple criterion to characterize connected sets. Even in the plane, there are sets for which it can be challenging to regocnize whether or not they are connected. The next example shows one such:
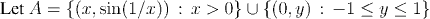

Is A connected or not? It's far from obvious whether or not it "falls naturally into two pieces". On the one hand it is naturally expressed as the disjoint union of two quite different sets. No point of the form (x, sin(1/x)) ever reaches the segment on the y axis. On the other hand, the curvy line is getting closer and closer to the y axis. So which do you think that it is?
Yes, I think the set is connected
No, I don't think it's connected
You'll notice that the proof of the last example used the fact that the continuous image of a connected set is connected. We haven't proved this yet, but it will be our next result.