Class Contents
Changing the Order of Summation
Rearrangements
The terms of a finite sum can be added in any order without changing the result, since addition is commutative. The same is not always true for infinite series! This seems very strange, and, if it is true, makes infinite series seem very wierd, pathological objects. The good news is that the the scope of this problem can be completely understood. There is one case where everything that can go wrong, does, and in the other case, there is no problem with adding the terms of the series in any order. The division between the well-behaved and the wild series is the division between absolutely and conditionally convergent series. First of all, let's decide what we mean by changing the order of addition of the terms of a series. If we add four real numbersthen there are 4!=24 ways of writing the terms in order, including the possibility of reversing the terms:
It doesn't seem reasonable to expect to reverse the order of the terms in an infinite series---there is no 'last' term to put first!

Example:

There's now a very nice split: Every conditionally convergent series can be rearranged so as to diverges, or even, to converge to any real value at all. In stark contrast, every absolutely convergent series can be rearranged freely, without affecting its convergence, or the value that it converges to in the least! The next two propositions set out the details of these facts.
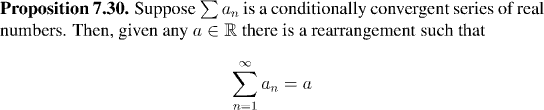
Remark:
Of course it takes quite a delicate argument to make a rearrangement of a conditionally convergent series converge to a given value. In general you shouldn't expect a rearrangement of a conditionally convergent series to converge at all. A conditionally convergent series can always be rearranged so as to diverge.

