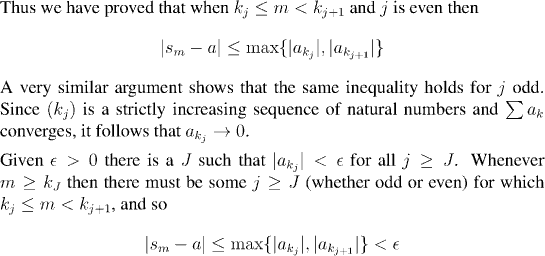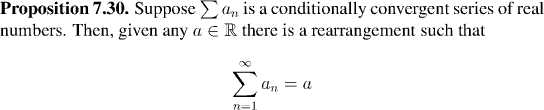
arrow_back This means that if we were to start at any point N and add up the positive terms after that point in order, then the partial sums would be unbounded above. Likewise if we added up the negative terms following N in order then the sequence of partial sums would be unbounded below. 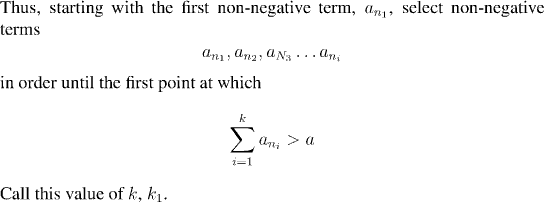Question: What happens if the very first term is already greater than a?

Question: How do we know that the sum ever reaches values greater than a?

Question: How do we know that the point k₁ is ever reached?

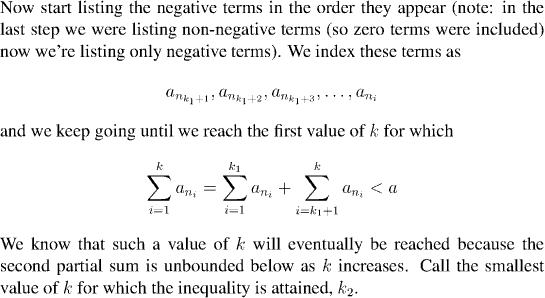
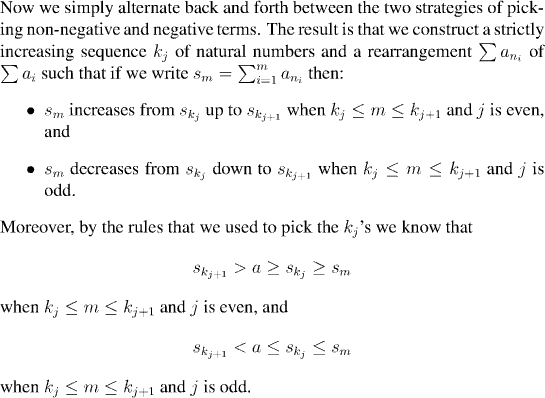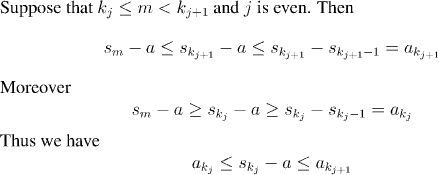
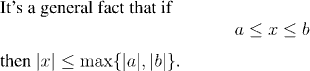It remains to put this all together and show that the partial sums s_m converge to a. Question: Try to prove this. (The simple properties of the absolute value function may help.)