arrow_back Alternate between picking the positive terms of the series for a while, then picking the negative terms. This produces a sequence of partial sums which alternately increase then decrease. Arrange that this oscillation takes place on either side of the number a, as shown:

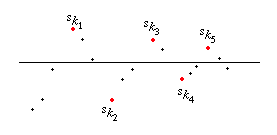
Moreover (as in the picture) make sure that the sequence of partial sums reverses its direction each time it crosses from one side of a to the other. Thus the partial sums are always within one term of the original series of a. Since the terms of the series converge to zero (the series is convergent) the partial sums of the rearranged series must converge to a.