Class Contents
Changing the Order of Summation
Double Series
Suppose our series are indexed by two natural numbers instead of just one, so that they look like:
We've already seen an example of this sort of thing, in the Cauchy Product Formula. There we were, essentially, studying
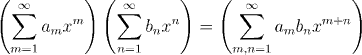
and the key ingredient was interchanging the order of summation. We shall look at the Cauchy Product formula in those terms again in a little while. First, let us think in more detail about what is meant by
We shall see that there is no one answer that is clearly right.
Remark:
We can plot the point (m,n) in the plane. Graphically, what we are doing is adding
up the terms for (m,n) on each of the columns, and then adding the results.
Equally well, we could choose to sum the terms along the rows first, and then add the results of that. That would amount to fixing n, and forming the series obtained by summing along n.
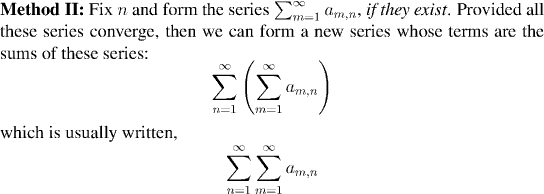These two methods of summation need not always give the same answer. In fact, one may converge,
while the terms of the other do not even exist:
Example:
For a third approach, we could sum all (m,n) with m and
n less than k and take the limit as k goes to
infinity.
This would have the advantage that only one limit is being computed, instead of infinitely many. Of
course this would still be true if we took any finite collection of terms and let the collection
grow so as to include all pairs (m,n). Put more precisely:
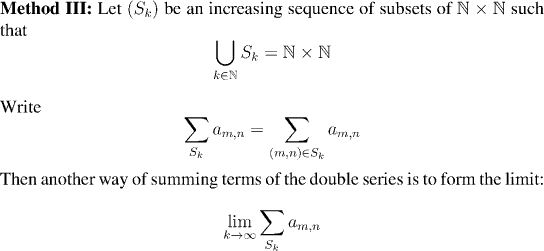
Remark:
The last method isn't really a single way of summing the series, but rather a whole class of
different methods corresponding to different choices of S_k's. Different choices for the increasing sequence of sets
(S_k) will result in the terms of the double series being taken in
different order. From the last section, we know that this will, most
likely affect the convergence of the series. We also know, however, that when a single series
is absolutely convergent, the order of summation does not matter. It turns out that the same is true
with double series.
Example:
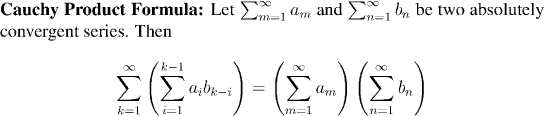
Note that the inner sum in this formulation runs from 1 to k-1. In our original statement of the Cauchy Product Formula the sum ran from 0 to k. This is simply because our absolutely convergent series in the original case started at zero (because they were modelled on power series) while now, our series start at 1.
Example:
