Class Contents
Riemann-Stieltjes Integration


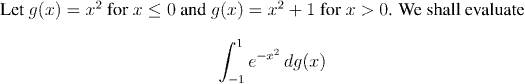
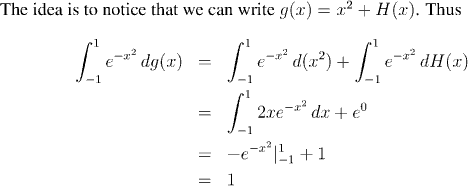
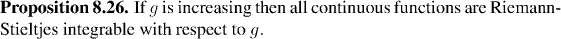
Now, it's easy to tell whether or not a function is increasing, but it's not so clear to tell whether or not a function is the difference of two increasing functions, unless you are actually told the increasing functions in question. For example:
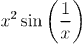
can be written as the difference of two increasing functions on [0,1], while
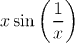
cannot be written as the difference of two increasing functions on [0,1].
Fortunately there is a beautiful criterion which allows us to tell whether or not a function can be expressed as the difference of two increasing functions. This is particularly useful for Riemann-Stieltjes integration because other results that hold for Riemann integration (such as the Triangle Inequality) only hold for Riemann-Stieltjes integration when the weight function is of this form.
The condition which tells when a function is the difference of two increasing functions is called bounded variation. Follow the link if you would like to learn more about functions of bounded variation:
Click here to learn more about bounded variation