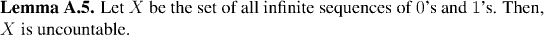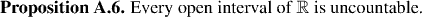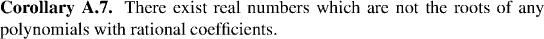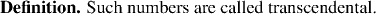Class Contents
Sets with the same cardinality
What does it mean for two sets to have the same number of elements? This is a simple question when the sets are finite, but when we come to examine it carefully we find that it gives us a way of saying what it means for two infinite sets to have the same number of elements. Perhaps very surprizingly, not all infinite sets have the same number of elements. In some sense, some "infinities" are bigger than others!If we think carefully about what we mean when we say two sets (assumed finite for the moment) have the same number of elements, we probably mean one of two things:
- If we were to count the sets, we'd get the same answer
- The sets can be lined up so that the elements are in one-to-one correspondance
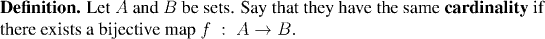
Example:
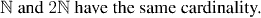
Remark:
In fact, the first of the two possible meanings of "two (finite)
sets have the same number of elements" that we suggested above
is not so far from the other one as might have at first appeared. After all,
counting the sets really boils down to finding a one-to-one correspondance between
the set and a suitable set {1,2,3,...,n} of natural numbers. If, when we count the sets
we find that we "get the same number" what we really mean is that both sets have a one-to-one
corresponadnce to the same set {1,2,3,...,n}. But, thus, there is a one-to-one
correspondance between the elements of the original two sets, and they have the same cardinality.
Example:
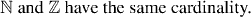
Remark:
These last two examples bring to mind a lovely
illustration of some of the strange behavior of infinite sets, known as
Hilbert's Hotel
.
Example:

Remark:
- The relation "have the same cardinality as" is an equivalence relation.
- The bijections used are far from unique - all that is needed is to find one, though.
Countable Sets
The most important distinction we usually need to make on the size of a set (after the distinction between finite and infinite sets) is between those which have the cardinality of the integers or a finite set and those which do not. We reserve a special name for sets of this type: we call them countable.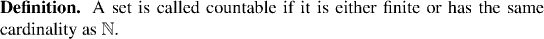
Remark:
Infinite sets are split into the countable and uncountable ones. If a
set is countable and infinite, then its elements can be listed as xn=f(n),
where f is a bijection between the set and the set of natural numbers.
The fact that you can always list, or
enumerate the elements of a countable set means you can work with them one at
a time - in fact, that is the real importance of countability for most considerations!
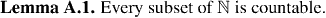
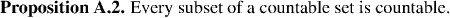
The next corollary uses Proposition A.2 to give three useful criteria for countablility. The importance of these criteria is that under appropriate conditions, we can use them to show that a set is countable by finding a map between the set and the natural numbers which need only be one-to-one, or perhaps onto, but need not be both. This has the effect of releiving us of some tedious details, and allowing us to focus on the essentials of whether or not a set is countable.

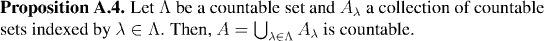
Remark:
This says a countable union of countable sets is countable.
The following set of examples use Proposition A.4 to build up larger and larger sets which
can be seen to be countable. The end of this chain of constructions will be to show that
the set of all reals which are the roots of polynomials with rational coefficients (the algebraic
numbers) are countable. Later, we shall use this fact to prove that there do exist numbers which are not algebraic.
Example:
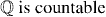
Example:
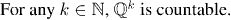
Example:
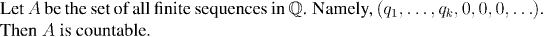
Example:
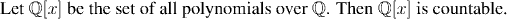
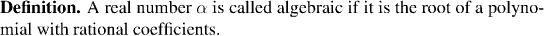
Example:
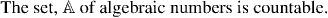
Remark:
Uncountable Sets