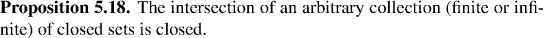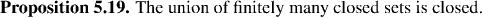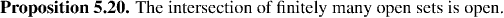arrow_back arrow_forward

Class Contents

Properties of Open and Closed Sets

We've already seen that all open balls are open sets (and this was analogous to the fact that open intervals in the real line are open sets). One of the first examples of closed sets that we saw in the real line was finite sets. It is also true that all finite subsets of a metric space are closed. One could prove this the same way that we proved in in the real line. However, a quicker proof is available if we use Proposition 5.12.

Proof.

The next four propositions are direct analogues of Propositions 2.7, 2.8, 3.15, and 3.16. Their proofs are also direct copies of the proofs of these results, and so they have been omitted.

Constructing and Recognizing Open and Closed Sets

Propositions 5.14 and Corollary 5.15 are very useful tools for constructing open and closed sets. The reason is that most of the sets that one works with in mathematics are specified in the following form:

On the other hand, the preimage of a set S under a function f is of the form:

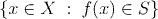
So, the basic principle to constructing open or closed sets or to recognizing that a given set is open or closed, is to rewrite the condition:

by finding:

a continuous function f, and
a set S (either open or closed)

so that the condition specifying the set is logically equivalent to the condition:

If S is open then, by Proposition 5.14, we have an open set, if S is closed then by Corollary 5.15, we have a closed set.

Of course the trick is finding the right function and the right open or closed set. The next few examples illustrate what's going on:

Example:

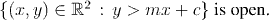
It remains to show that the function f(x,y)=y-mx-c is continuous, and that the set S is open. Of course we know that open intervals are open in the real line so S is certainly open. To see that f is continuous we use the sort of arguments that we developed in the section: Convergence and continuity in Euclidean spaces.

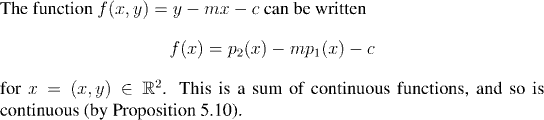
Note:

It was very easy to see that the set S was open. This is because the open intervals in the real line provide us with a plentiful supply of sets we know to be open. For this reason we usually aim to have the functions we construct for this type of argument always map into the real numbers.

Likewise, we know that closed intervals in the real line are closed sets so when we want to show a set is closed we usually try to get a function which maps into a closed interval in the real line.

Example:

The set

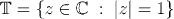
is closed.

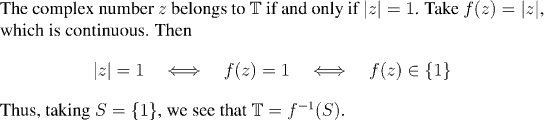
Question: Why is S closed?

Example:

The set

is open.

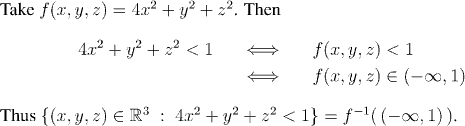
The set S of all real numbers less than 1 is open, because it is an open interval.

Question: Why is f continuous?