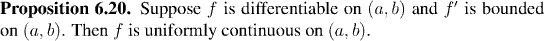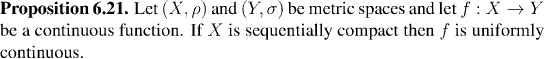Class Contents
Uniform Continuity
We'll start by re-examining the definition of continuity for a function between two metric spaces.
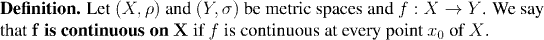
Of course this rather begs the question, so recall also the definition of continuity at a point:
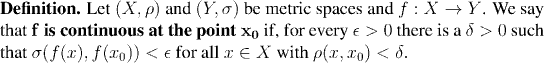
Now we pose the question: What does delta depend on?
Clearly we expect that the smaller epsilon is, the smaller we will have to take delta. But since x0 was set before we started to look for delta, the chances are that the value of x0 we are given will affect what delta we need just as much as epsilon does. The next example shows exactly how that sort of thing can happen:

Remarkably enough, oftentimes for functions that crop up in practice it is possible to find values of delta which work for a given epsilon and for all x0. When this happens we say that the function is uniformly continuous.
The reason that this remarkable, and frequently useful, property is fairly common, is tied up in sequential compactness. We start with a formal definition of uniform continuity.
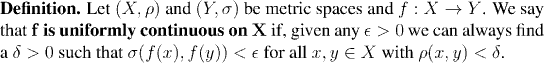
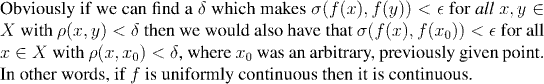

There is a simple graphical interpretation of uniform continuity. We saw in an interactive demo that a function was continuous at a point x0 if, given a fixed height epsilon, we could always choose a narrow enough width delta, so that the curve never passed through the ceiling or floor of the box of height epsilon, and width delta, centered on (x0, f(x0)).
By the same token, we can say that f is uniformly continuous if, given a diameter of epsilon we can always cut a tube of diameter epsilon to short enough a length (namely, delta) that it can run freely along the curve withough bumping into the sides of the tube. The following picture illustrates this idea:
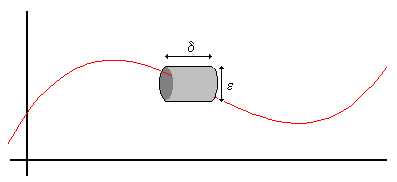
From this point of view, it is clear that one thing which could cause a continuous function to fail to be uniformly continuous would be is the slope of the line becomes too large. The following theorem shows that, conversely, if the slope is never too large, the function must be uniformly continuous.
This last result relies on differentiability, and is only applicable to real-valued functions on the real line. The following result shows why uniform continuity is in fact a very common property, despite being, apparently, much stronger than simple continuity. Not surprisingly, the key ingredient is sequential compactness.
The function f(x)=x^{1/2} is uniformly continuous on (0,1), even though it has an unbounded derivative on that interval.

In the next section we shall introduce the definition of compactness (as opposed to sequential compactness), and show that the two definitions are, in fact, equivalent.