Class Contents
Compact Sets
So far we have talked exclusively about sequentially compact sets. There is another, apparently very different, property which subsets of a metric space may have, which is called compactness. In this class we shall introduce that property and show that it is equivalent to sequential compactness.

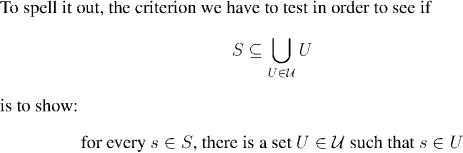

The example above drives home the important observation that an open cover can have vastly more sets in it that are needed to cover the set S. For example in the last case, the set R3 was one of the sets in the cover, and it served to contain all three points of S on its own.
A set is compact if whenever we cover it with infinitely many open sets, there is always enough redundancy in the covering that we can select finitely many of the covering sets to do the job. The definitionbelow makes this precise:

We can summarize this by saying that a set is compact if every open cover has a finite subcover.
Every finite set is compact.

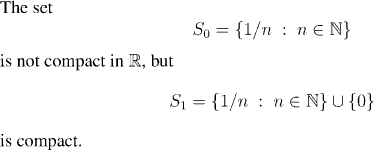
As an example of how the property of compactness proves useful in practice, we shall obtain an alternate proof of Proposition 6.21.
Note that this really is an alternate proof of a result we already know, rather than, as you might suspect, a new result. Although the hypotheses in the two statements are different (this example assumes that the domain is compact; Proposition 6.21 assumed that the domain was sequentially compact), the hypotheses ammount to the same. This is because compact metric spaces and sequentially compact metric spaces are exactly the same things. Our main effort in the next class will be devoted to proving this deep fact.
