arrow_back There are two big problems with the argument we just outlined, but both of them can be overcome, with the appropriate theorems. Series aren't exactly like finite sums, and the series

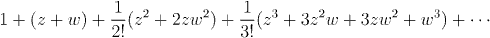
might not might not even converge, much less converge to the same value as the product of E(z) and E(w).

We only looked at the first few terms of the product. We need to prove that as a general rule, if we multiply together the terms of E(z) with the terms of E(w) and group together all the terms with the same total order, then we get the term of E(z+w) of the same order. The first problem will be overcome using Proposition 7.7, and the second one will be overcome in Corollary 7.8, using the Binomial Theorem.