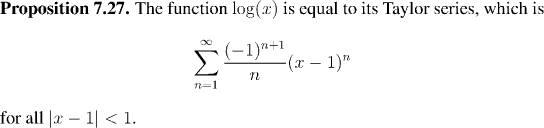

Remark:
The case of 0 < x < 0.5 does not succumb to this analysis, however. That isn't to say
that the remainder term from Taylor's theorem doesn't converge to zero; in fact it
does, as we will know once we have proved (by other means) that log(x) is
equal to its power series. What we can say, however, is that the information Taylor's
theorem provides us with is insufficient to prove that that remainder term goes to zero.
As we have indicated, another approach is needed. We shall follow a similar line of
argument as in the
case of xa
.
