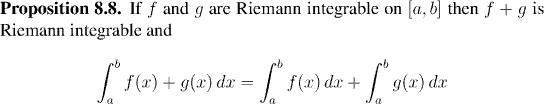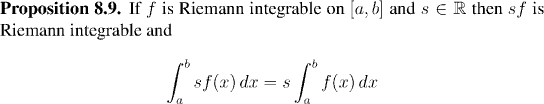Class Contents
Properties of the Integral
We have seen two examples of families of real numbers which are indexed by partitions of [a,b]: the upper and the lower Riemann sums. Moreover, we defined convergence for these families in a way which makes us think of them as "generalized sequences". It'll be useful to push this concept a little further in the direction of generality: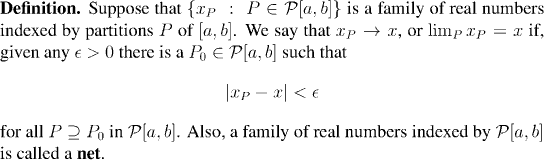
Having a notion of generalized sequences and their convergence is all very well as far as it goes. But the thing which made convergent sequences so useful to us was the rule for arithmetic of sequences that we developed in Chapter 3. All these arithmetic results for sequences have direct analogues for nets. We shall state a couple of them, and prove the most useful:
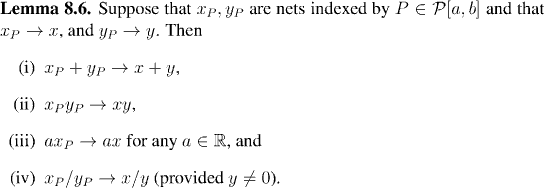
Factoid:
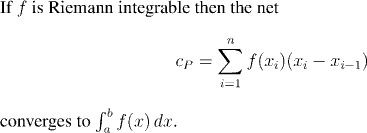
(For the proof, just apply Lemma 8.7 to the upper and lower Riemann sums.)
