arrow_back arrow_forward

Class Contents

• Evaluating the integral

Evaluating the Integral

Although we have defined the integral, and shown that our definition is broad enough to extend to all continuous functions, we have not yet seen the integral evaluated for a single function! We shall calculate the integral of a couple of simple functions using only the definition. The purpose of that exercise is really to underline how impossibly hard to use the definition of the integral actually is. In order to effectively compute the integrals of more complicated functions, the most powerful tool at our disposal is the Fundamental Theorem of Calculus, which essentially shows that integration is the opposite of differentiation.

We start by computing the integral of a step function. It is perfectly clear what the "area under the curve" of this function is, so our expectation is that the definition of the integral will be consistent with that. (It would be a big problem with our definition, if it didn't agree in this case!)

Proof.

One (admittedly trivial) consequence of this is the integral of a constant function:

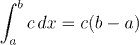
The next example is instructive because it shows how difficult it is to compute the integral directly (using only the definition) for even one of the simplest functions. There is clearly a pressing need for a more powerful tool for evaluating integrals!

Proof.

Proof.

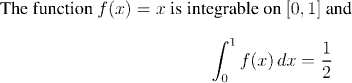
The Fundamental Theorem of Calculus truly deserves its name! At one stroke, we have acquired the ability to compute a huge range of integrals. In fact all of the techniques of integration that you learn in the traditional college calculus sequence (including integration by parts, and change of variable) just boil down to clever applications of the Fundamental Theorem. Simply for the sake of seeing how to implement this, we shall perform one standard "calculus-style" integration:

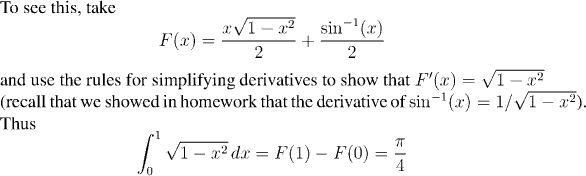
Note that although the direct verification that F(x) has the right properties is routine, it's unlikely anyone would have guessed ahead of time that this is the right function to use. The techniques of integration exist to help us make the right guesses or deductions about what the correct function corresponding to a given f(x) might be. We shall see more of the techniques later, but for the moment we continue to develop the theory.